SLA Engine Component
Summary
The SLA Engine represents the component responsible for generating, storing and observing the formal documents describing electronic agreements between the parties involved in CloudSocket: BPaaS bundle customers, brokers and cloud providers. The component follows the WS-Agreement specification. This means that the documents representing templates and agreements are valid according to the schema defined in the specification. The specification is extended where needed to cover some specific CloudSocket needs.
This component will expose:
- A graphical user interface for checking the status of agreements,
- A REST API interface allowing programmatic access to the different types of functionalities offered.
The main functionalities are:
- Generation of WS-Agreement templates and agreements.
- Management of SLA related entities: templates, agreements, providers, violations, penalties
- Assessment of SLOs and corresponding penalties when an SLO is violated.
- Notification of detected violations and incurred penalties to interested parties.
- ...
| Type of ownership | Extension & Adaptation |
| Original tool | SLA Framework asset |
| Planned OS license | Apache License Version 2.0. |
| Reference community | None |
Consist of
- SLA Engine (core functionalities)
- SLA Dashboard (Graphical User Interface)
- SLA Generator (generates WS-Agreement compliant documents)
Depends on (uses or used-by dependencies)
- Monitoring Engine
- Allocation Environment
- Marketplace
- Cloud Provider Engine
Component responsible
| Developer | Company | |
|---|---|---|
| Roman Sosa Gonzalez | roman.sosa@atos.net | Atos |
| Joaquin Iranzo | Joaquin.iranzo@atos.net | Atos |
Architecture design
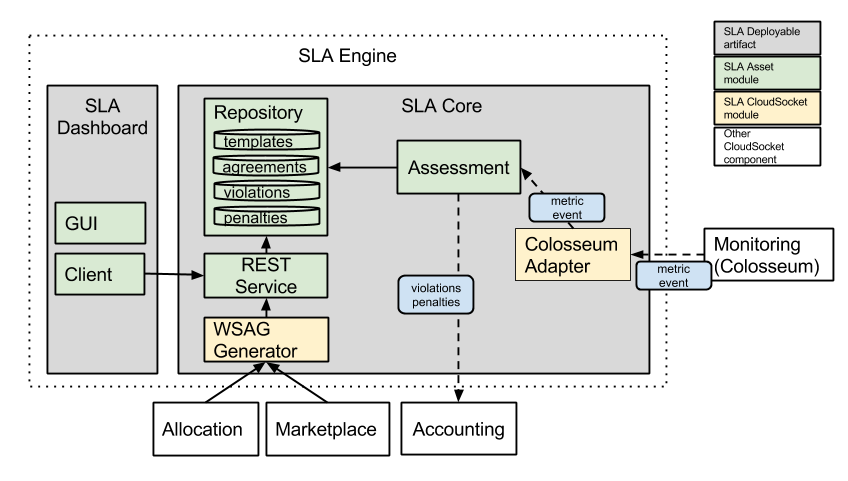
Figure: General architecture for SLA Engine
The SLA Engine in CloudSocket is composed of three main components:
- SLA Core. It relies on the Atos SLA Framework asset, with some CloudSocket-related modules. It contains all the basic functionality. The main subcomponents are:
- Repository. Database of WSAG related entities.
- Assessment. It is in charge of the evaluation process of the SLA agreements. It notifies raised violations and penalties to interested observers (i.e., an Accounting component).
- REST Service. It is the REST interface of the SLA Core to the world.
- WSAG Generator. It generates WSAG-compliant templates and agreements according to the requirements of allocation and marketplace, respectively.
- Colosseum Adapter. It is charge of: i) subscribing into Colosseum to the appropriate metric events, and ii) to receive events and translate them into the internal SLA representation.
- SLA Dashboard. This component is a frontend application where the user/admin can check the status of agreements and the penalties that have been applied.
The related components with the SLA Engine in CloudSocket are:
- Monitoring. It reports the metric data to the SLA Core.
- Allocation. The Allocation Environment contacts the SLA Generator to obtain a template that describes the service level of a BPaaS Bundle.
- Marketplace. It shows a human-readable description of a BPaaS Bundle SLA to the customers.
- Cloud Provider Engine. It pProvides the SLA to be stored and managed by the SLA Engine.
Installation manual
Development
Requirements
- Oracle JDK >= 1.7
- Database to install the database schema for the service: Mysql>=5.0
- Maven >= 3.2
- Python >=2.7
Installation
- Download source code from gitlab
git clone https://omi-gitlab.e-technik.uni-ulm.de/cloudsocket/sla-framework.git cd sla-framework
- Create database in mysql
$ mysql -p -u root mysql> CREATE DATABASE atossla; mysql> CREATE USER atossla@localhost IDENTIFIED BY '_atossla_'; mysql> GRANT ALL PRIVILEGES ON atossla.* TO atossla@localhost;
- Compile SLA Engine
( cd sla-core && mvn clean install )
- Execute sla-core server. The following command will start an SLA Engine server in port 8080.
sla-core/bin/runserver.sh [port]
- Execute sla-dashboard server. The following commando will start an SLA Dashboard server in port 8000
sla-dashboard/bin/runserver.sh
Production
Requirements
- Oracle JRE >= 1.7
- Database to install the database schema for the service: Mysql>=5.0
- Python 2.7
- Virtualenv
Installation
Create the database like done in Development section.
The script `dist/bin/make-dist.sh` creates an archive file with the necessary scripts and artifacts to run the SLA Engine in a server.
dist/bin/make-dist.sh scp dist/target/sla-framework.tar.gz server: # replace 'server' with the ip/name of server ssh server: tar xzf sla-framework.tar.gz cd sla-framework virtualenv ~/virtualenvs/sla-dashboard ( . ~/virtualenvs/sla-dashboard/bin/activate && cd lib/sla-dashboard && pip install -r requirements.txt && ./manage.py migrate ) bin/start-sla-core-service.sh bin/start-sla-generator-service.sh bin/start-sla-dashboard-service.sh
To stop the services:
bin/stop-sla-core-service.sh bin/stop-sla-generator-service.sh bin/stop-sla-dashboard-service.sh
Environment variables
The SLA Engine execution can be configured with the use of environment variables. The list of recognized env vars and their default values is:
SLA_CORE_HOST (127.0.0.1), SLA_CORE_PORT (8080): sla-core listening address; passed to sla-dasboard.SLA_DASHBOARD_HOST (127.0.0.1). public hostname of SLA Dashboard; it must be reached by IDM component.SLA_DASHBOARD_PORT (8000): sla-dashboard listening port.SLA_GENERATOR_HOST (127.0.0.1), SLA_GENERATOR_PORT: sla-generator listening address.DB_URL (jdbc:mysql://localhost:3306/atossla): A jdbc connection string in the formatjdbc:mysql://${IP}:${PORT}/${DB}.CLOUDIATOR_URL (http://127.0.0.1:9000/api): URL of Cloudiator REST API.SLA_URL (http://127.0.0.1:8080/api): Public address of SLA Engine REST API; used in subscriptions to Monitoring Engine in order to receive metric notifications.IDM_CLIENT_ID (""): SLA Engine Client ID for OAuth2 authorization flow.IDM_CLIENT_SECRET (""): SLA Engine secret for OAuth2 authorization flow.IDM_AUTHORIZE_URL (http://csmarket.ymens.com:9090/oauth/authorize): Authorization URL in OAuth2 authorization flow.IDM_TOKEN_URL (http://csmarket.ymens.com:9090/oauth/token): Token URL in OAuth2 authorization flow.
User manual
API Specification
The generic API is in SLA Framework API.
The lifecycle of the SLA in CloudSocket is shown in the diagram below. 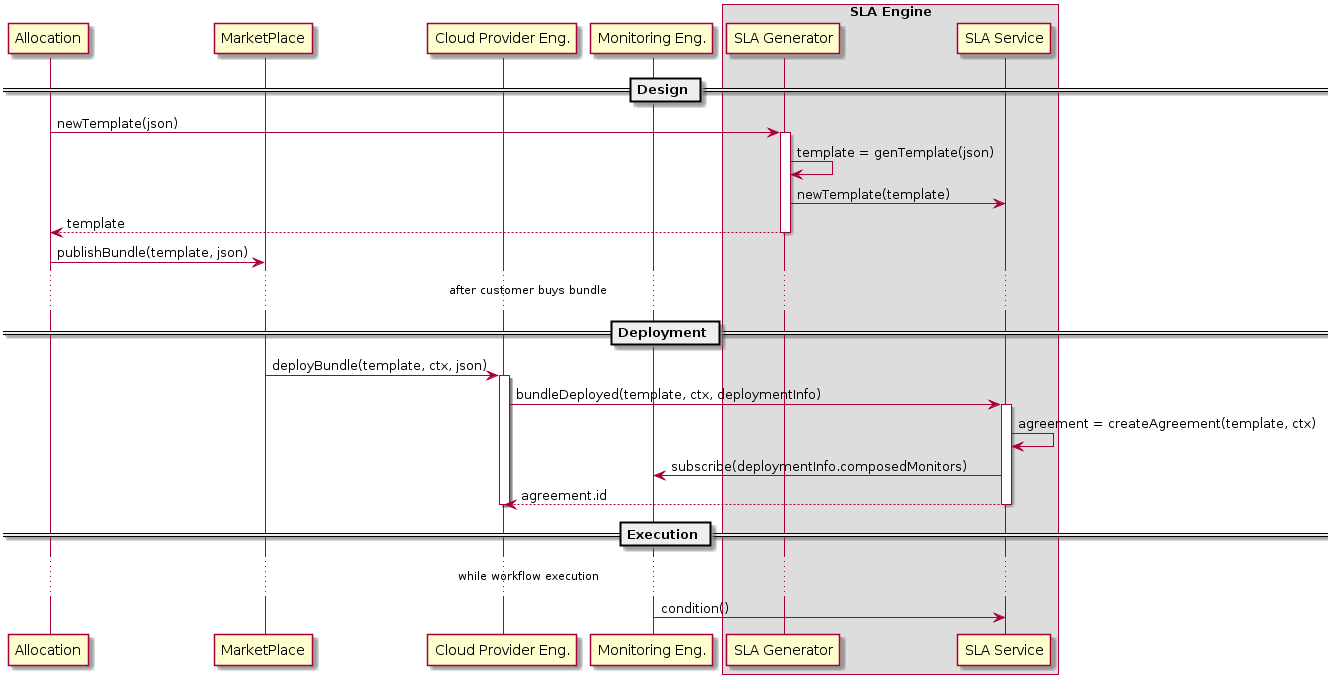
Figure: SLA Sequence Diagram
Specific CloudSocket API is explained below:
Generate a template
POST /api/templates
This endpoint takes a simplified JSON definition of a WS-Agreement template and returns the WS-Agreement template, which can be fed into the SLA Core.
An input example: JSON Input for Christmas bundle
The penalties element are described in the SLA Core developer guide (search for Business Rules).
Example:
curl -X POST http://134.60.64.232:8001/api/templates -d@./cs-wsag-generator-service/src/test/resources/json_christmas.json -H"Content-type:application/json"
The input file is:
{
"templateName" : "Sending Christmas Greetings (with SLA) SLA Template",
"bpaasBundle" : "Sending Christmas Greetings (with SLA)",
"broker" : "bwcon",
"assessment" : "bwcon",
"monitoring" : "bwcon",
"guaranteeTerms" : [ {
"name" : "KPI Hourly CPU_GuaranteeTerm",
"sloDescription" : "Hourly Usage of CPU should be less than 80%",
"penaltiesDescription" : "3 penalties occurs in one day => 1€ discount on the current month",
"slo" : {
"condition" : "KPIHourlyCPU",
"context" : "MeanCPU",
"comparison" : "LE",
"threshold" : 80.0
},
"penalties" : [ {
"count" : 3,
"interval" : "P1D",
"penalty" : {
"type" : "discount",
"expression" : "1.00",
"unit" : "euros",
"validity" : "P1M"
}
} ]
} ]
}
The output is:
<?xml version="1.0" encoding="UTF-8" standalone="yes"?>
<wsag:Template xmlns:cs="http://wsag.sla.cloudsocket.eu" xmlns:sla="http://sla.atos.eu" xmlns:wsag="http://www.ggf.org/namespaces/ws-agreement" wsag:TemplateId="3b4d79ba-307f-40aa-a139-b925efe1149d">
<wsag:Name>Sending Christmas Greetings (with SLA) SLA Template</wsag:Name>
<wsag:Context>
<wsag:AgreementResponder>bwcon</wsag:AgreementResponder>
<wsag:ServiceProvider>AgreementResponder</wsag:ServiceProvider>
<sla:Service>Sending Christmas Greetings (with SLA)</sla:Service>
<cs:context>
<cs:assessment>bwcon</cs:assessment>
<cs:monitoring>bwcon</cs:monitoring>
</cs:context>
</wsag:Context>
<wsag:Terms>
<wsag:All>
<wsag:GuaranteeTerm wsag:Name="KPI Hourly CPU_GuaranteeTerm">
<wsag:ServiceLevelObjective>
<wsag:KPITarget>
<wsag:KPIName>KPI Hourly CPU_GuaranteeTerm_kpi</wsag:KPIName>
<wsag:CustomServiceLevel>
<cs:slo>
<cs:constraint>MeanCPU LE 80.000000</cs:constraint>
<cs:conditionConstraint>KPIHourlyCPU NOT EXISTS</cs:conditionConstraint>
<cs:description>Hourly Usage of CPU should be less than 80%</cs:description>
</cs:slo>
</wsag:CustomServiceLevel>
</wsag:KPITarget>
</wsag:ServiceLevelObjective>
<wsag:BusinessValueList>
<wsag:CustomBusinessValue count="3" duration="P1D">
<sla:Penalty type="discount" expression="1.00" unit="euros" validity="P1M"/>
<sla:description>3 penalties occurs in one day => 10€ discount on the current month</sla:description>
</wsag:CustomBusinessValue>
</wsag:BusinessValueList>
</wsag:GuaranteeTerm>
</wsag:All>
</wsag:Terms>
</wsag:Template>
The CloudSocket sequence diagram is depicted in figure.
Generate an agreement
POST /cloudsocket/api/agreements
This endpoint generates an agreement from a template and the needed information context. It is intended to be called when a bundle has been deployed. Both provider (if not yet), template (if not yet) and agreement are stored in SLA Core.
It receives the template in the body, and the context information (currently, only the customer ID) in headers.
Headers:
- customer ID: X-CloudSocket-Customer
Example:
curl -X POST -d@sla-service/src/test/resources/samples/template02.xml -H"X-CloudSocket-Customer: customer-a" http://134.60.64.232:8080/cloudsocket/api/agreements -H"Content-type:application/xml"
Input body: Template
X-CloudSocket-Customer header: customer-a
The output is:
4679e474-2322-4da2-be75-a0004c7f8df8
Start evaluation
PUT /cloudsocket/api/enforcements/{agreementId}
This endpoint makes the appropriate subscriptions to the Monitoring Engine and starts the evaluation of the agreement. It is intended to be called just after the CreateAgreement endpoint.
The body contains a CsEnforcementJob. A serialized example is found in https://omi-gitlab.e-technik.uni-ulm.de/cloudsocket/sla-framework/blob/master/sla-core/sla-service/src/test/resources/samples/cs-enforcementjob2.json
It returns the enforcement entity in /api/enforcements/{agreementid} in the body.
Example:
curl -X PUT -d@sla-service/src/test/resources/samples/cs-enforcementjob2.json http://localhost:8080/cloudsocket/api/enforcements/agreement-id -H"Content-type:application/json" -H"Accept:application/json"
Input body:
{
"agreementId" : "agreement-id",
"enabled" : true,
"composedMonitorIds" : [ 1, 2, 3 ]
}
Output:
{"agreementId":"agreement-id","enabled":true}
CloudSocket extensions to WS-Agreement
There is a number of extensions that have been made to the WS-Agreement specification in order to obtain the CloudSocket objectives:
Context
It is desirable to explain in an SLA which are the entities that are to be involved under which context and role. In the case of the broker acting as a service provider, the broker may outsource some tasks to other entities (e.g., monitoring, execution, evaluation) so supporting parties can also be involved in the SLA.
Taking advantage of the xs:any child of wsag:Context element, a cs:context element has been defined to support the declaration of additional entities in the SLA: assessment and monitoring, at this moment.
CustomServiceLevel
An SLO should include all appropriate information that can assist in its proper monitoring, at least:
- definition of the metric
- schedule
- measurement window
- object being monitored
- evaluation frequency
In the case of CloudSocket, the metric and SLO are proper and completely defined in the CAMEL document. The SLOs in the SLA document reference the CAMEL entities.
The figure below is a simplified class diagram of the implied CAMEL entities in the description of SLO in the SLA document.
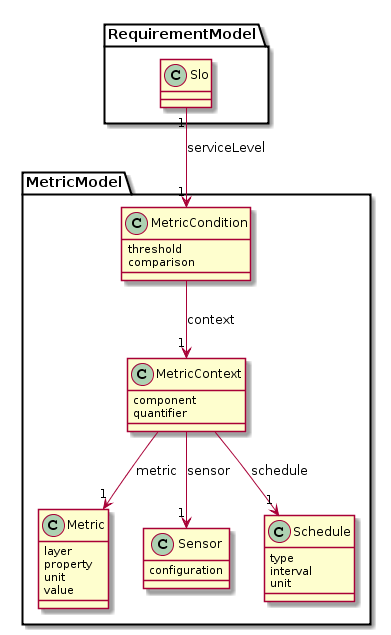
The Monitoring Engine allows the SLA Engine to subscribe to calculations of a MetricContext. Then, the constraint is:
constraint : metric_context operator threshold metric_context : <metric_context_id> operator : LT | LE | EQ | GE | GT threshold : <double>
A cs:slo element describe the CloudSocket SLOs.
Besides the constraint, a cs:slo may contain a human description (shown in marketplace) of the SLO and a window description.
This is an example of an SLO:
<wsag:GuaranteeTerm wsag:Name="HourlyResponseTimeLessEqual20msConditionGuaranteeTerm">
<wsag:ServiceLevelObjective>
<wsag:KPITarget>
<wsag:KPIName>ResponseTimeLessEqual20msConditionGuaranteeTerm_kpi</wsag:KPIName>
<wsag:CustomServiceLevel>
<cs:slo>
<cs:constraint>ResponseTimeCompositeMetricContext LE 20.000000</cs:constraint>
<cs:description>the mean of response time in 1 hours should be always less or equal than 20ms</cs:description>
</cs:slo>
</wsag:CustomServiceLevel>
</wsag:KPITarget>
</wsag:ServiceLevelObjective>
<wsag:BusinessValueList>...</wsag:BusinessValueList>
</wsag:GuaranteeTerm>
Business values
Penalties apply when an SLO is not fulfilled. SLA Service allows to define several penalties according to the number of occurrences of the violation in an interval of time, defined by the count and interval properties: if "count" violations occur in "interval" time, the penalty applies.
The SLA Engine defined a generic way to define a penalty. A penalty is composed of the following properties:
- Type (string): it is the type of the penalty. For example: "discount", "support".
- Expression(string)
- Unit (string): together with 'expression' represent the value of the penalty. F.e. (100, €) or ("telephone", null) if type="support".
- Validity (xs:duration): the time the penalty applies. F.e., if there is a discount of (10, %) and validity is 1 month, the discount is applied over the monthly price. Assume we have a penalty "free_telephone_support"; the validity will be the time this free support will be available.
The penalties are described in the sla:penalty elements, which are inside a wsag:CustomBusinessValueElement.
An example is below:
<wsag:GuaranteeTerm wsag:Name="HourlyResponseTimeLessEqual20msConditionGuaranteeTerm">
<wsag:ServiceLevelObjective>...</wsag:ServiceLevelObjective>
<wsag:BusinessValueList>
<wsag:CustomBusinessValue count="1" duration="P1D">
<sla:Penalty type="discount" expression="10.00" unit="eur" validity="P1M"/>
<sla:description>if 1 violation occurs in 1 day => apply a discount of 10euro for the current month</sla:description>
</wsag:CustomBusinessValue>
</wsag:BusinessValueList>
</wsag:GuaranteeTerm>
The definition of penalties is not responsibility of the SLA Engine.
The SLA Engine do not handle penalties internally. It detects when they should be raised and communicates them to observers.
Example
A full example of an SLA agreement with CloudSocket extensions follows:
<wsag:Agreement wsag:AgreementId="b705c5c9-bafa-4f8b-8079-09be96173995" xmlns:wsag="http://www.ggf.org/namespaces/ws-agreement" xmlns:sla="http://sla.atos.eu" xmlns:cs="http://wsag.sla.cloudsocket.eu">
<wsag:Name>Send Invoice IaaS Europe SLA Template</wsag:Name>
<wsag:Context>
<wsag:AgreementInitiator>84a5e594-f4ce-4daa-ac1e-3ebe032ca97c</wsag:AgreementInitiator>
<wsag:AgreementResponder>bwcon</wsag:AgreementResponder>
<wsag:ServiceProvider>AgreementResponder</wsag:ServiceProvider>
<wsag:TemplateId>94bafed5-335f-4ce3-98f5-e0c57b844997</wsag:TemplateId>
<sla:Service>Send Invoice IaaS Europe</sla:Service>
<cs:context>
<cs:assessment>bwcon</cs:assessment>
<cs:monitoring>bwcon</cs:monitoring>
</cs:context>
</wsag:Context>
<wsag:Terms>
<wsag:All>
<wsag:GuaranteeTerm wsag:Name="NinjaInvoiceHourlyRamLessEqual70PercentageConditionGuaranteeTerm">
<wsag:ServiceLevelObjective>
<wsag:KPITarget>
<wsag:KPIName>NinjaInvoiceHourlyRamLessEqual70PercentageConditionGuaranteeTerm_kpi</wsag:KPIName>
<wsag:CustomServiceLevel>
<cs:slo>
<cs:constraint>NinjaInvoiceHourlyRamCompositeMetricContext LE 70.000000</cs:constraint>
<cs:conditionConstraint>NinjaInvoiceHourlyRamLessEqual70PercentageCondition NOT_EXISTS</cs:conditionConstraint>
<cs:description>the mean of ram of ninja invoice in 1 hours should be always less or equal than 70%</cs:description>
</cs:slo>
</wsag:CustomServiceLevel>
</wsag:KPITarget>
</wsag:ServiceLevelObjective>
<wsag:BusinessValueList>
<wsag:CustomBusinessValue count="1" duration="P1D">
<sla:Penalty type="discount" expression="10.00" unit="eur" validity="P1M"/>
<sla:description>if 1 violation occurs in 1 day => apply a discount of 10€ for the current month</sla:description>
</wsag:CustomBusinessValue>
</wsag:BusinessValueList>
</wsag:GuaranteeTerm>
<wsag:GuaranteeTerm wsag:Name="NinjaInvoiceHourlyResponseTimeLessEqual20msConditionGuaranteeTerm">
<wsag:ServiceLevelObjective>
<wsag:KPITarget>
<wsag:KPIName>NinjaInvoiceHourlyResponseTimeLessEqual20msConditionGuaranteeTerm_kpi</wsag:KPIName>
<wsag:CustomServiceLevel>
<cs:slo>
<cs:constraint>NinjaInvoiceResponseTimeCompositeMetricContext LE 20.000000</cs:constraint>
<cs:conditionConstraint>NinjaInvoiceHourlyResponseTimeLessEqual20msCondition NOT_EXISTS</cs:conditionConstraint>
<cs:description>the mean of response time in 1 hours should be always less or equal than 20ms</cs:description>
</cs:slo>
</wsag:CustomServiceLevel>
</wsag:KPITarget>
</wsag:ServiceLevelObjective>
<wsag:BusinessValueList>
<wsag:CustomBusinessValue count="1" duration="P1D">
<sla:Penalty type="discount" expression="10.00" unit="eur" validity="P1M"/>
<sla:description>if 1 violation occurs in 1 day => apply a discount of 10€ for the current month</sla:description>
</wsag:CustomBusinessValue>
</wsag:BusinessValueList>
</wsag:GuaranteeTerm>
</wsag:All>
</wsag:Terms>
</wsag:Agreement>
Further analysis
This section elaborates about our research on some additions to the specification that were not finally implemented on the prototype. Special thanks to Kyriakos Kritikos (FORTH).
Cost model
The following information can be expressed for a cost model. The proposed structure is:
Pricing
- minPrice: minimum price threshold. The price can never go below this threshold, irrespectively of the number of discounts that are legitimate to be claimed by the service customer.
- maxPrice: maximum price threshold. Similarly, the service requester is guarded by this threshold in case of rewards such that he/she will never have to pay more than this threshold for a certain billing period.
- basePrice: base price for the service. This is the normal price not affected by any discount or reward.
- priceUnit: the currency for the service price (e.g., euros, dollars, etc.).
Charging
- Charging frequency (duration - every 1 hour, 1 day, 1 month, etc)
- Charging description (human-oriented description of what is charged - could be more elaborate on a technical level to explain how the price is calculated - could also provide links to web pages where this information is much detailed)
- Reservation type: on-demand, advanced reservation, spot prices
Billing
- Billing frequency (duration - every month, every 6 months, every year, etc.)
- Billing means (credit card, bank transfer, paypal)
- Billing process description (human-oriented description of how billing should be performed)
The excerpt below shows an example of a cost model expressed in WS-Agreement.
<cs:priceModel name="Service Price Model">
<cs:pricing maxPrice="90" minPrice="40" basePrice="0.1" priceUnit="euros"/>
<cs:charging frequency="1H" reservationType="on-demand">
<cs:description>service is charged every 1 hour of use</cs:description>
</cs:charging>
<cs:billing frequency="1M" means="credit-card,paypal">
<cs:description>the customer has to first provide the credit card details which will then be charged based on the charging frequency according to the actual cost incurred in the billing period</cs:description>
</cs:billing>
</cs:priceModel>


